on
Huffman Algorithm
대학교의 자료구조 시간에 압축 관련한 알고리즘을 들은 적이 있다. 가장 유명하다고 알려진 것이 허프만인데 아무래도 책에 있는 그림으로 알고리즘을 공부하기에 그림만 보아서는 어떻게 코드로 구현할지 그 당시엔 감이 오지 않았다. 생각해보면 그림만 보고서 코딩을 한다는 게 당연히 어렵고 그렇다고 인터넷을 참조해보아도 엄청나게 긴… 코드만 쳐다보다 바로 창을 꺼버리게 되어 항상 이해만 할 뿐 코드로서 잊혀진 알고리즘이었다.
하지만 최근에 아는 지인으로부터 허프만 관련한 세미나를 요청하여 의지를 가지고 공부하였는데 생각보다 그렇게 어려운 방법은 아니ㄷ… 항상 처음이 중요한 거 같다..
그래서 이번 포스팅은 대학교 때 듣고 지나쳐온 허프만 알고리즘을 소개하고자 한다.
우선, 컴퓨터에서는 어떻게 데이터를 저장할 것인가를 생각해보자
예를 들어, ABABCA라는 문자열을 저장할 경우 아래와 같을 것이다.
우선 가장 간단하고 기본적인 방법 문자는 아스키코드로 표현할 수 있으며, 이진수로 변형되어 컴퓨터에 저장된다.
| 문자 | 아스키코드 | 이진수 |
|---|---|---|
| A | 65 | 01000001 |
| B | 66 | 01000010 |
| C | 67 | 01000011 |
위 표에 따라 문자열 ABABCA는
| A | B | A | B | C | A |
|---|---|---|---|---|---|
| 01000001 | 01000010 | 01000001 | 01000010 | 01000011 | 01000001 |
8 * 6개 = 48bit으로 저장 된다는것인데…
사용되지 않는 문자까지 비트에 포함되어 매우 비효율적인 저장 방식이 될 것이다.
하지만 이런 비효율적인 저장 방식을 해결하고자 허프만의 방식은 자주 등장하는 문자는 작은 비트로 할당하여 저장하자라는 압축 알고리즘이다.
아래 표와 같이 문자에 비트를 할당해보자
| 문자 | 아스키코드 | 이진수 |
|---|---|---|
| A | 65 | 0 |
| B | 66 | 01 |
| C | 67 | 11 |
| A | B | A | B | C | A |
|---|---|---|---|---|---|
| 0 | 01 | 0 | 01 | 11 | 0 |
9bit로 저장되어 압축률은 9/48인 약 18.75%로 압축하여 저장이 가능하다. 정말 합리적이지 않은가?
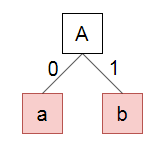
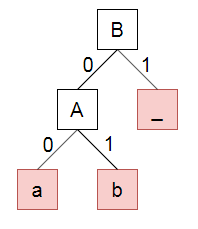
그렇다면 자주 등장하는 문자를 어떻게 효율적으로 비트를 지정해야 할까?
해당 방법은 허프만 트리로 해결 가능하다.
허프만 트리를 구성하기 위한 Flow
- 문자열에 등장하는 문자들의 출현 빈도수를 카운팅
- 빈도수로 정렬
- 빈도수가 낮은 두개를 묶어서 트리형태로 만든다.
- 해당 두개를 합산한 트리를 정렬에 포함
- 다시 정렬
- 모든 문자를 참조할때까지 1~5번 반복
2~5번의 경우 우리에게 필요한 것은 가장 작은 빈도수를 가진 2개이기에 매번 loop에 Quick Sort를 하면서 정렬하는 것 보다 Min hip을 이용한 방식이 효율적이다.
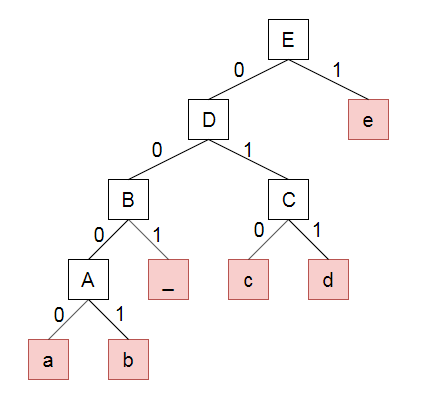
우선, aa_bb_cccc_dddd_eeeeeeee 문자열을 허프만 트리로 만드는 예시를 코드와 함께 보자
- 문자열에 등장하는 문자들의 출현 빈도수를 카운팅
#include <vector>
vector<int> countASCII(string s) {
const short ASCII_SIZE = 128;
vector<int> ascii(ASCII_SIZE, 0);
for (int i = 0; i < s.size(); i++) ascii[s[i]]++;
return ascii;
}
카운팅 방법은 어렵지 않으며 아스키코드의 크기만큼 메모리 할당 후 출현에 따른 카운팅을 한다.
- 빈도수로 정렬
Min Hip을 직접 구현 할수 있지만 STL의 도움을 받자 허프만은 트리 구조이기에 Node를 생성하면서 트리를 구성하는게 편하다.
struct Node {
char m;
int count;
Node* left;
Node* right;
Node(char m, int count, Node* left = NULL, Node* right = NULL)
: m(m), count(count), left(left), right(right) {};
Node(Node* a, Node* b)
: m('T'), count(a->count + b->count), left(a), right(b) {};
};
Node는 문자, 카운트 수, 자식들 포인터 할 변수 2개로 구성되어 있다. 그리고 생성의 편리를 위해 위와 같이 생성자를 구성하였다. 하나는 일반 생성, 3~4번을 처리하기 위한 생성자다.
Min Hip은 아래의 코드로 구현한다.
struct compare {
bool operator()(Node* t, Node* u) {
return t->count < u->count;
}
};
//priority_queue< Node*, vector<Node*>, compare > pq;
반복을 통해서 최종 트리를 생성해보자.
#include <queue>
Node* makeHuffmanTree(string s) {
vector<int> countAscii = countChar(s);
priority_queue< Node*, vector<Node*>, compare > minq;
for (int i = 0; i < countAscii.size(); i++)
if (countAscii[i]) minq.push(new Node(i, countAscii[i]));
while (minq.size != 1) {
Node* ta = minq.top(); minq.pop();
Node* tb = minq.top(); minq.pop();
minq.push(new Node(ta, tb));
}
Node* root = minq.top(); minq.pop();
return root;
}
- 입력받은 Count Array는 Node로 변경하고, Min Hip에 Push 해서 자동 정렬 시킨다.
- 상위 2개의 Node를 받고 2개의 Count를 합산한 새로운 Node를 다시 Push 한다.
- Min Hip 이 1개 남을 때까지 반복
Reference
Hax hip : https://twpower.github.io/93-how-to-use-priority_queue-in-cpp